Zum vorherigen Abschnitt
Zum Inhaltsverzeichniss
|
Zum vorherigen Abschnitt
|
Zum Inhaltsverzeichniss
|
Zum nächsten Abschnitt
|
Die Abschirmung erfolgt durch eine geschlossene Hülle aus absorbierenden Materialien um die Störquelle /-senke. Das bedeutet, elektrische Felder werden z.B. durch eine geerdete Hülle aus leitfähigen Materialien um die feldverursachende Ladung abgeschirmt. Des Weiteren würde man die Ecken und Kanten, falls möglich, abrunden, um die Feldstärke an diesen Stellen zu reduzieren bzw. niedrig zu halten, falls die Umhüllung sich doch auflädt. Magnetische Felder sind deutlich schwerer abzuschirmen da sie im Prinzip nur durch ein gleichstarkes Gegenfeld neutralisiert werden können. Zum Glück treten Magnetfelder an Computern (außer an Bildschirmen) im Vergleich zu anderen elektrischen (Haushalts-)Geräten selten auf. Ebenfalls möglich wäre eine Abschirmung, die dem B-Feld durch ständiges Wechseln der Magnetisierungsrichtung Energie entzieht und in Wärme umwandelt (Anhang B, Beschreibung der verwendeten Abschirmmaterialien). Elektromagnetische Wellen werden, wie E-Felder, durch eine leitende Umhüllung "absorbiert". Diese Hülle muß nicht geerdet sein und darf sogar "Lücken" z.B. für Kabeldurchführungen besitzen (mit d << lambda ). Für den Ort der Abschirmung gibt es zwei Strategien, entweder möglichst nahe an der Störquelle /-senke oder eine Abschirmung um die Gesamtanlage. Auf Computer bezogen hieße das, daß man entweder eine einzelne besonders empfindliche Komponete wie etwa den Prozessor oder eine besonders stark strahlende Komponente wie das Netzteil einzeln abschirmt oder eine Umhüllung um den gesamten Computer verwendet, was aufgrund entfallender Platzprobleme leichter möglich wäre, aber mehr Material verbrauchen würde.
Die statischen elektrischen Felder kann man allgemein mit einem Influenz-E-Feldmesser messen, homogene Wechselfelder mittels des Verschiebestroms zwischen zwei gegeneinander und gegen Erde isolierten Elektroden. Für die TCO-Messung wird eine Meßsonde folgenden Aufbaus verwendet.
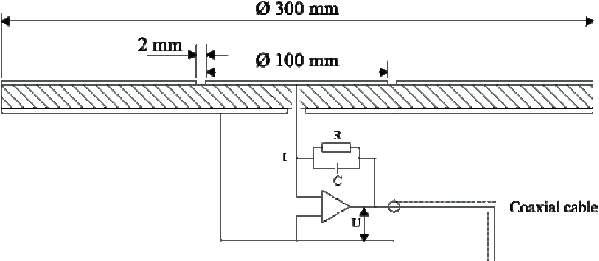
Zwei kreisförmige (r=0,15 m) Kupferfolien sind durch einen
einige Millimeter dicken Isolator getrennt. Auf der dem
Meßobjekt zugewandten Seite ist eine innere Kreisfläche
(r=5cm) durch einen 2mm breiten Spalt vom umgebenden Kreisring
getrennt. Zur Messung wird die Rückseite und der
äußere Kreisring der Vorderseite an der Abschirmung des
Koaxialkabels angeschlossen und damit geerdet, und die kleine
Kreisscheibe auf der Vorderseite wird über einen
Operationsverstärker mit kapazitiver Rückkopplung als
Meßverstärker angeschlossen. Im elektrischen Wechselfeld
kommt es bei dieser Anordnung zu Verschiebeströmen, die
über den Operationsverstärker vorverstärkt werden und
dann mit einem Meßverstärker und einem daran
angeschlossenen Milliamperemeter gemessen werden. Man misst also
quasi permanent den Auf-/Entladestrom der Meßfläche
gegenüber Erdpotential. Die Stärke des E-Feldes ergibt sich
dann zu
Dabei ist U die Spannungsdifferenz zwischen Erde und Kreisscheibe, C die
Kapazität des Meßverstärkers, A die Fläche
der Kreisscheibe und
ist die elektrische Feldkonstante. Herleiten läßt sich diese
Formel über folgende
Zusammenhänge
:
,
und
.
Es gilt nämlich, daß
und
.
Daraus ergibt sich
und damit die oben angegebene Formel.
Vor der Messung wird die Sonde im homogenen Feld eines
Plattenkondensators bei Frequenzen von 16 - 1000 Hz bzw. 15-120kHz
und Feldstärken von 2,5 bis 250 V/m geeicht.
Statische Felder mißt man über Hallsonde, Wechselfelder
über Spule oder Rahmenantenne unter Verwendung des
Induktionsstromes. In den Meßvorschriften der TCO sind drei
zylindrische, rechtwinklig zueinander angeordnete Spulen mit 116mm
Durchmesser vorgeschrieben. Die Resonanzfrequenz der Meßsonde
muß außerhalb des zu messenden Bandes liegen und durch
Widerstände möglichst weit abgedämpft sein. Diese
Vorschrift liegt in der physikalischen Beobachtung begründet,
daß ein schwingungsfähiges System bei seiner
Resonanzfrequenz auch bei einer sehr geringen Zufuhr von Energie zu
sehr starken Schwingungen angeregt werden kann. Es könnte also
passieren, daß sehr geringe magnetische Felder, die aber die
Resonanzfrequenz der Meßsonde treffen, das System soweit
aufschaukeln, bis ein falscher, da viel zu hoher Meßwert
abgelesen wird. Die Vorschrift, daß die Meßsonde durch
Widerstände abgedämpft werden muß, die Resonanzkurve
also flachgehalten werden soll, ist aus folgendem Grund sinnvoll. Ein
schwingungsfähiges System läßt sich bei gleicher
Anregungsamplitude mit Frequenz in der Nähe der Resonanzfrequenz
deutlich besser zu Schwingungen anregen, als mit Frequenzen, die sich
deutlicher von der Resonanzfrequenz unterscheiden. Wenn die
Resonanzfrequenz nun knapp oberhalb der oberen Grenze des
Meßfilters und des zu messenden Frequenzbandes läge,
würden hohe Frequenzen das System deutlich stärker anregen
und damit unverhältnismäßig stark in den Meßwert
eingehen. Wenn man aber mit Widerständen die Resonanzkurve stark
abdämpft, dann ist die Frequenzabhängigkeit der
Empfindlichkeit nicht mehr zu registrieren bzw. nicht mehr
störend, da sehr schwach ausgeprägt. Vor der Messung wird
die Sonde im sinusmäßig modulierten quasi homogenen Feld
eines Helmholtzspulenpaares bei Frequenzen von 16 -1000 Hz bzw.
15-120kHz und Flußdichten von 25 - 2000 nT geeicht. Das
Meßprinzip ist hier, daß eine Änderung im Magnetfeld
eine Induktionsspannung in der Spule erzeugt. Dabei ist die Höhe
der Spannung proportional zur Ableitung der Magnetfeldstärke B nach
der Zeit. Da auch die Geschwindigkeit der änderung bekannt ist
(also die Frequenz bzw. Periodenlänge des magn. Feldes und der
induzierten Spannung ), kann man unter der Annahme, daß die
Feldstärke einem sinusartigen Verlauf folgt, auch den
Spitzenwert des Feldes angeben. Diese vereinfachende Annahme trifft
auf die Magnetfelder eines Computers / Monitors sogar relativ gut zu.
Die Feldstärke B ergibt sich hier zu:
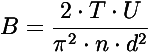Dabei ist T die Periodendauer des magn. Wechselfeldes, U ist die
Induktionsspannung, n die Windungszahl der Spule und d der
Durchmesser der Spule. Diese Formel ergibt sich aus den folgenden
Ansätzen: Laut Formelsammlung ist
und
.
Für die Querschnittsfläche der (zylindrischen) Meßspule
gilt:
Aus der folgenden Abbildung ergibt sich:
.
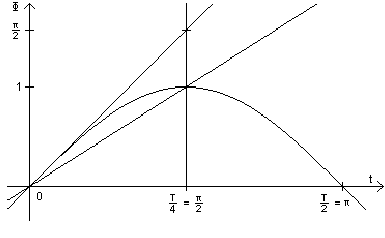
Daraus folgt:
.
|
Zum vorherigen Abschnitt
|
Zum Inhaltsverzeichniss
|
Zum nächsten Abschnitt
|